크기 (Cardinality)
정의 : 집합 A의
크기(cardinality)는 iff 집합 B와 일대일 대응(bijection)인 경우만 집합 B와 동일하며 $\mid A \mid = \mid B \mid$로 표현된다
A에서 B로의 일대일 함수(Injection)가 있는 경우, A의 cardinality가 B의 cardinality보다 작거나 같다. 이를 $ \mid A \mid \le \mid B \mid$ 로 쓴다
$ \mid A \mid \le \mid B \mid$ 이고 $A$와 $B$가 다른 cardinality를 가졌다면, A의 cardinality가 Bdml cardinality보다 작다고 하고 $\mid A \mid < \mid B \mid$라고 한다
Countable
정의 : 단사(injective) 함수 $S → Z^+$가 존재할 때, 집합 $S$를
가산(countable)이라고 한다집합 $A$가 countable하다면, 유한하거나 $Z^+$와 같은 cardinality를 가진다
집합이 countable하지 않다면,
불가산(uncountable)하다고 한다
예를 들어 $R$은 uncountable한 집합이다
countable한 무한한 집합의 cardinality를 $ \aleph_0 $(aleph null)으로 표현한다 ($ \mid S \mid = \aleph_0 $)
집합이 Countable함을 보이기
무한 집합은 집합의 원소를 sequence(양수의 인덱스를 가지는)로 나열할 수 있는 경우에만 셀 수 있다
정수 집합에서 집합 $S$로의 일대일 대응 함수 f는 $a_1, a_2, … a_n, …$ 등으로 표현 할 수 있다 (where $ a_1 = f(1), a_2 = f(2), …$)
예제 1
짝수인 양의 정수의 집합 $E$가 countable set인지 보이기
풀이
$f(n) = 2n$이라고 하자
- $1 ↔ 2$
- $2 ↔ 4$
- $3 ↔ 6$
- $…$
- $n = 2n$
함수 $f$ 는 일대일(injective) 함수이자 onto(surjective) 함수이기 때문에 일대일 대응(bijection)이 된다
- 일대일(injective)임을 보이기 위해 $f(n)=f(m)$이라고 하자. 그럼 $2n=2m, n=m$이 된다
- onto(surjective)임을 보이기 위해 $t$가 짝수인 양의 정수라고 하자. 그럼 양수인 $k$에 대해 $t = 2k$이고 $f(k)=t$가 된다
예제 2
정수의 집합 $Z$가 countable set인지 보이기
풀이
sequence(수열)로 나열할 수 있다
\[0,1,-1,2,-2,3,-3,...\]다음과 같이 $N$에서 $Z$로 가는 일대일대응(bijection) 함수를 정의할 수 있다
\[f(n) := \begin{cases} \frac{n}{2} & (\text{n is even}) \\ -\frac{n-1}{2} & (\text{n is odd}) \\ \end{cases}\]양의 유리수가 countable함을 보이기
유리수는 두 정수 $p, q (q \neq 0)$로 표현할 수 있다
예제 3
양의 유리수가 countable함을 보여라
풀이
0을 제외한 자연수의 ordered pair $(m, n)$는 유리수 $\frac{m}{n}$에 해당한다
반대로, 모든 유리수 $\frac{m}{n}$은 ordered pair $(m, n)$에 해당한다
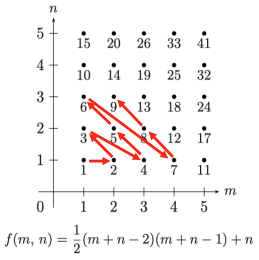
0이 아닌 자연수의 모든 ordered pair의 집합 $N^* \times N^$에서 0이 아닌 자연수의 집합 $N^$으로 대각선을 따라 $(1,1), (2,1), (1,2), (3,1), (2,2), (1,3) …*$ 순으로 가는 bijection 함수 $f$는 다음과 같다
\[f(m,n) = \frac{1}{2} (m + n - 1)(m + n - 2) + n\]문자열 (Strings)
예시 4
유한한 알파벳 $A$에 대한 유한한 문자열 집합 $S$가 countably infinite함을 보여라
풀이
문자열을 sequence로 나타낼 수 있음을 보이면 된다
- 길이가 0인 모든 문자열을 알파벳 순서로 나열한다
- 길이가 1인 모든 문자열을 알파벳 순서로 나열한다
- 길이가 2인 모든 문자열을 알파벳 순서로 나열한다
- $…$
예시 5
모든 자바 프로그램이 countable함을 보여라
풀이
문자열이 countable함과 동일하게 보이며 아래의 과정이 추가된다
- 가져온 문자열을 Java 컴파일러에 입력한다
- 컴파일이 성공하면, 구문상 올바른 Java프로그램이며, 해당 프로그램을 목록에 추가한다
- 다음 문자열을 확인한다
실수가 uncountable함을 보이기
예시
실수가 uncountable함을 보여라
풀이
다음 과정을 대각선 논법(Cantor's diagnalization argument)이라고 한다
- $R$이 countable하다고 하자. 그럼 $0$과 $1$사이 실수 또한 countable하다 (countable set의 부분집합 또한 countable하기 때문)
- 0부터 1까지의 실수를 $r_1, r_2, r_3, …$과 같이 나열한다
- 소수를 다음과 같이 나타낼 수 있다 $r_i = 0.d_{i1}d_{i2}d_{i3}d_{i4}…, \text{ where } d_{ij} \in [9]_0$
- 다음을 이용해 실수 r을 만든다 \(r = e_1e_2e_3... \text{ with } e_i = \begin{cases} 3 & (d_{ii} \neq 3) \\ 4 & (d_{ii} = 3) \end{cases}\)
- 이 소수 $r$은 $r_1, r_2, r_3, …$ 어느것과도 일치하지 않는다. 왜냐하면 i번째 소수의 위치가 $r_i$와 다르기 때문이다. 따라서, 0과 1 사이의 모든 실수는 자연수로 열거할 수 없다
- $R$의 부분집합이 uncountable하므로 $R$도 uncountable하다
COMPUTABILITY
WIP DN_05 p.108