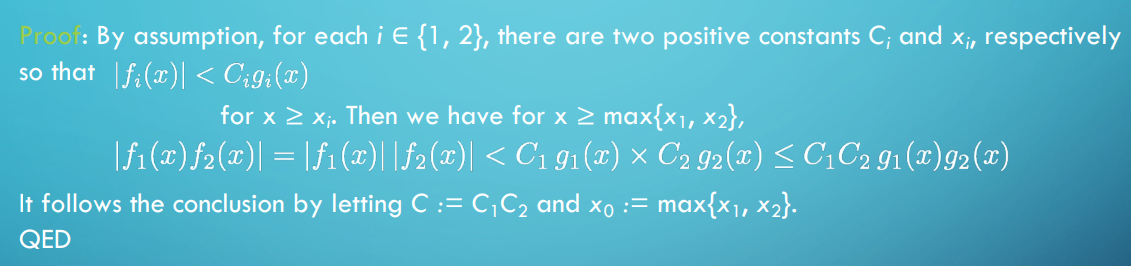The Growth of Functions
컴퓨터 과학과 수학에서 함수가 얼마나 빨리 성장하는지 관심을 갖는 경우가 많다
그 이유로
- 동일한 문제를 해결하기 위해 둘 이상 알고리즘의 효율성을 비교할 수 있다
- 입력이 증가함에 따라 특정 알고리즘을 사용하는것이 실용적인지 여부도 결정할 수 있다
The Big O Notation (점근 표기법)
정의 : $f$ 와 $g$를 양의 실수의 무한한 부분 집합에 대해 정의된 함수라고 하고, $g$는 $x$의 충분히 큰 모든 실수 값에 대해 엄밀히 양수라고 가정한다.
$x > x_0$일 때마다 $ \mid f(x) \mid \le C g(x) $ 가 되는 양의 상수 $C$와 $x_0$가 있다면 $f$는 $O(g)$라고 한다.
읽는 방법
- $f$ is big-O of $g$
- $f \in O(g)$
if $f \in O(g)$, then $\frac{ \mid f(x) \mid }{g(x)} $ is bounded for $x > x_0$.
Big-O 표기법에 대한 중요한 사항
상수 $C$와 $x_0$ ($=k$)는 $f \in O(g)$ 관계에 대한 근거값(witness)라고 한다
일단 한 쌍의 근거값이 필요하지만, 한 쌍을 찾는다면 무한히 많은 쌍의 근거값이 존재한다
“$f(x)$ is $O(g(x))$” 대신 $f(x) = O(g(x))$로 표기 될 수 있다
- $f(X) \in O(g(x))$가 더
일반적으로, 항상 양수 값을 취하는 함수를 다루기 때문에 f(x)의 절대값 기호를 지우고 쓴다
###
예제 1
함수 $f(x) = x^2 + 2x + 1$ 에 대해, $O(x^2)$ 을 보여라
$\mid x \mid > 1$ 일 때, $x^2 > \mid x \mid > 1$ 임을 알고 있다
따라서,
\[|f(x)| = \mid x^2 + 2x + 1 \mid \le \mid x^2 \mid + \mid 2x \mid + \mid 1 \mid < x^2 + 2x^2 + x^2 = 4x^2\]따라서, $x > x_0 = 1$ 일 때 $ \mid f(x) \mid < 4x^2 $ 이다
예제 1의 확장
$f(x) = x^2 + 2x + 1 \in O(x^2)$
예제 2
$7x^2$ is $O(x^3)$ 임을 보여라
- When $x > 7$ 일 때, $7x^2 < x^3$ 이다. 근거값 $C = 1$이고 $k = 7$이다
$n^2$ is not $O(n)$ 임을 보여라
$n > n_0$일 때마다 $ \mid n^2 \mid = n^2 \le Cn$ 인 상수 $C$와 $k$가 있다고 가정하자.
양변을 $n$으로 나누면, 모든 $n > n_0$에 대해 $n \le C$여야 하며, 터무니없다
다항식에 대한 Big-O 추정
정리 : $f(x) = a_n x^n + a_{n-1} x^{n-1} + … + a_1x + a_0$ 인 다항식 함수는 $ a_n \ne 0 $ 일 때 복소수이다
증명 :
$x > 1$ 이고
Assume that $x > 1$ and apply the triangle inequality for complex numbers, then since x > 1, so xk > 1 for all k ∈ [n]0, we have??
Big-O 추정 for some important functions
예시 1
첫 n개의 양수의 합을 Big-O 표기법을 이용해 추정해라
답
모든 자연수 $n > 1$ 에 대해,
\[1 + 2 + 3 + ... + n < n + n + ... + n = n^2\]이므로 첫 n개의 양수의 합에 대한 함수는 $n > 1$일 때 $O(n^2)$ 이다
예시 2
펙토리얼 함수를 Big-O 표기법을 이용해 추정해라
답
모든 자연수 $n > 1$에 대해
\[n! = n (n-1) (n-2) ... 3 \times 2 \times 1 = n^n\]이므로 $n > 1$에 대해 $n!$ is $O(n^n)$ 이다
예시 3
모든 $b > 0 \text{ and } b \ne 1$에 대해 $log_bn!$ 을 Big-O 표기법을 이용해 추정하라
$n! \le n^n$ 임을 알고 있으므로
$log_bn! = log_bn^n = n log_b n$ 이다
따라서, $log_bn!$ is $O(n log_bn)$ 이다
유용한 Big-O 추정
- $d > c> 1$ 이라면, $n^c$ is $O(n^d)$, but “$O(n^d)$ is not $n^c$”
- $b > 1$ 이고 $c$와 $d$가 양수라면, $(log_bn)^c$ is $O(n^d)$, but $n^d$ is not $(log_bn)^c$
- $b > 1$ 이고 $d$가 양수라면, $n^d$ is $O(b^n)$, but $b^n$ is not $O(n^d)$
- $c > b > 1$ 이라면, $b^n$ is $O(c^n)$, but $c^n$ is not $O(b^n)$
Combination of Functions
- if $f \in O(g_i)$ for $i \in \set{1,2}$, then $f_1 + f_2$ is $O(max \set{g_1, g_2})$
증명
For assumption, 각 $i \in \set{1,2}$에 대해, 두 개의 양수인 상수 각각 $C_i$와 $x_i$가 있고, 따라서 $\mid f_i(x) \mid < C_i g_i(x)$ 이다
$x \ge x_i$ 일 때, 우리는 $x \ge \max \set{x_1, x_2}$ 를 가진다
… WIP (DN_06_48)
- if $f_i$’s are both $O(g)$ for $i \in \set{1,2}$, then $f_1 + f_2$ is $O(g)$
*증명: * 1과 동일
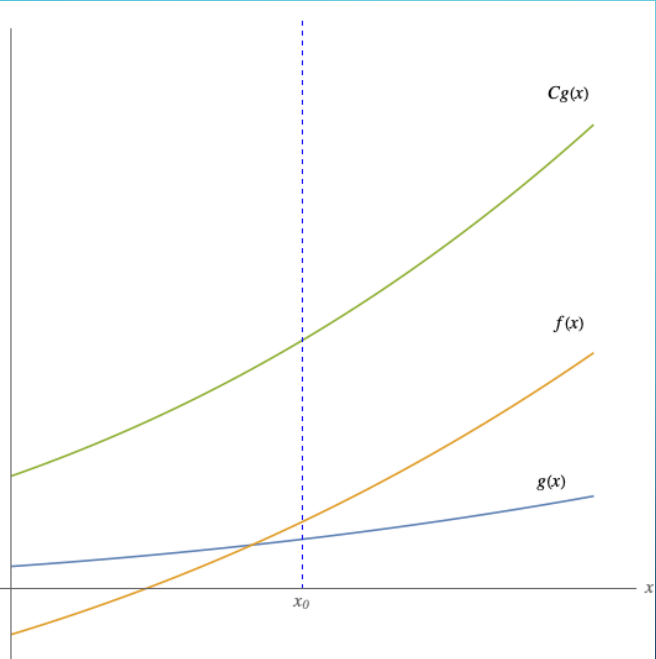
- if $f_i \in O(g_i)$ for $i \in \set{1,2}$, then $f_1 f_2$ is $O(g_1 g_2s)$
증명