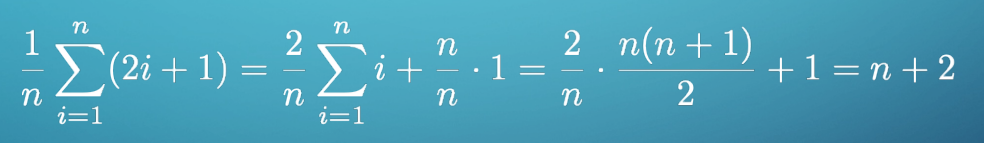시간 복잡도 (Time Complexity)

예시 1 : 최대값 구하기

다음 알고리즘의 시간복잡도를 계산하라

풀이

$\max < a_i $ 비교 연산은 $n-1$ 번 반복된다
$i$가 증가할 때마다, $i \le n$ 인지 확인하기 위한 테스트 수행
마지막 비교를 통해 $i > n$ 가 결정된다
정확히 $2 (n-1) + 1 = 2n - 1$번의 비교가 이뤄진다

그러므로 이 알고리즘은 $Θ(n)$ 이다

예시 2 : 선형 탐색의 최악 성능

다음 알고리즘의 시간복잡도를 계산하라

풀이

각 스탭마다 두번의 비교를 한다
루프의 마지막에 한번의 비교 $i \le n$가 일어난다
루프가 끝나고 한번의 비교 $i \le n$가 일어난다

if $x=a_i$, 2i+1 번 비교가 사용된다.

if $x$ not in list, 2n + 1 비교가 일어나고, 추가 비교를 사용해 루프를 종료한다.

따라서, worst case는 $2n + 2$번 비교가 일어난다. 그러므로 $Θ(n)$이다

예시 3 : 선형 탐색의 평균 성능

x=a_i$라면 2i+1 번 비교가 사용되므로 평균 성능은 다음과 같다

따라서 $Θ(n)$ 이다

예시 4 : 이진 탐색의 최악 성능

풀이

$n = 2k, k = log_2n$ 이라 가정한다

각 스탭마다 두번 비교한다
첫번째 반복에서 목록의 크기가 $2^k$이고 반복 후에는 $2^{k-1}$이다
이후 크키가 $2^1$이 될 때까지 반복한다
마지막 단계의 비교에서 목록의 크기는 $2^0=1$이고, 해당 요소는 나머지 단일 요소와 비교된다

그러므로 최대 $ 2k + 2 = 2 \log_2n + 2$ 번의 비교가 수행된다

따라서 시간복잡도는 $Θ(\ln n)$ 이며, 선형 탐색보다 낫다

예시 5 : Bubble sort의 최악 성능

각 목록을 통해 $n-1$ 번의 pass가 생긴다
각 pass마다 $n-i$ 비교가 수행된다

\[\sum_{i=1}^{n-1} = \frac{n(n-1)}{2}=\frac{1}{2}n^2-\frac{1}{2}n\]

따라서 최악의 경우 시간복잡도는 $Θ(n^2)$ 이다

예시 6 : Insertion sort의 최악 성능

총 비교 횟수는 다음과 같다

\[\sum^{n}_{i=2} = \frac{n(n+1)}{2} - 1 = \frac{n^2+n-2}{2}\]

따라서 최악의 경우 시간복잡도는 $Θ(n^2)$ 이다

예시 7 : Matrix Multiplication 알고리즘

두 $n \times n$ 행렬을 곱하기위해 정수의 덧셈과 정수의 곱셈을 몇번 사용하는가?

풀이

$n^2$번의 반복이 있다. 각 entry마다 $n$번의 곱셈과 $n-1$번의 덧셈이 있다. 그러므로 $n^3$번의 곱셈과 $n^2(n-1)$ 번의 덧셈이 사용된다

따라서 시간복잡도는 $Θ(n^3)$ 이다

예시 8 : Boolean Product 알고리즘

얼마나 많은 비트연산이 사용되는가?

풀이

$n^2$번의 반복이 있다. 각 entry마다 $n$번의 OR과 $n$번의 AND 연산이 있다. 그러므로 $n^3$번의 OR과 AND연산이 사용된다

따라서 시간복잡도는 $Θ(n^3)$이다

Matrix-Chain Multiplication

$A_1$ is $30 \times 20$, $A_2$ is $20 \times 40$, $A_3$ is $40 \times 10$ 일 때, 가장 적은 곱셈 연산을 수행하는 순서를 찾아라

풀이

두 가지 방법이 있다

$A_1(A_2A_3)$
- $A_2A_3$은 $20 \times 40 \times 10 = 8000$ 연산이 필요하며, $A_1$ 와 $(A_2A_3)$ 은 $30 \times 20 \times 10 = 6000$ 번의 연산이 필요하며 총 $8000+6000 = 14000$ 번의 연산이 필요하다
$(A_1A_2)A_3$
- $A_1A_2$은 $30 \times 20 \times 40 = 24000$ 번의 연산이 필요하고 $(A_1A_2)A_3$ 은 $30 \times 40 \times 10 = 12000$ 번의 연산이 필요하므로 총 $24000+12000=36000$번의 연산이 필요하다

따라서 첫번째 연산이 더 적은 연산을 필요로 한다

Algorithmic prardigms (절차적 처리안의 전형)

Algorithmic prardigms (절차적 처리안의 전형)은 다양한 문제를 해결하기 위한 알고리즘을 구성하기 위해 특정 개념을 기반으로 하는 일반적인 접근 방식이다

greedy algorithms
brute-force algorithms
divide-and-conquer algorithms
dynamic algorithms
probabilistic algorithms

Brute-force algorithm

평면의 n개 점 집합에서 가장 가까운 점 쌍을 찾기위한 무차별 대입 알고리즘을 구성하고 worst-case에 대한 시간복잡도 계산하기

풀이

brute-force 알고리즘은 단순히 모든 점 쌍 사이의 거리를 계산하고 거리가 가장 작은 쌍을 선택한다

알고리즘은 다음과 같다

$\frac{n(n-1)}{n}$ 번 반복한다
반복 동안 한번의 비교 연산이 있다

이 알고리즘의 시간복잡도는 $Θ(n^2)$ 이다

이산수학 | 계산복잡도 (Complexity of Algorithm)