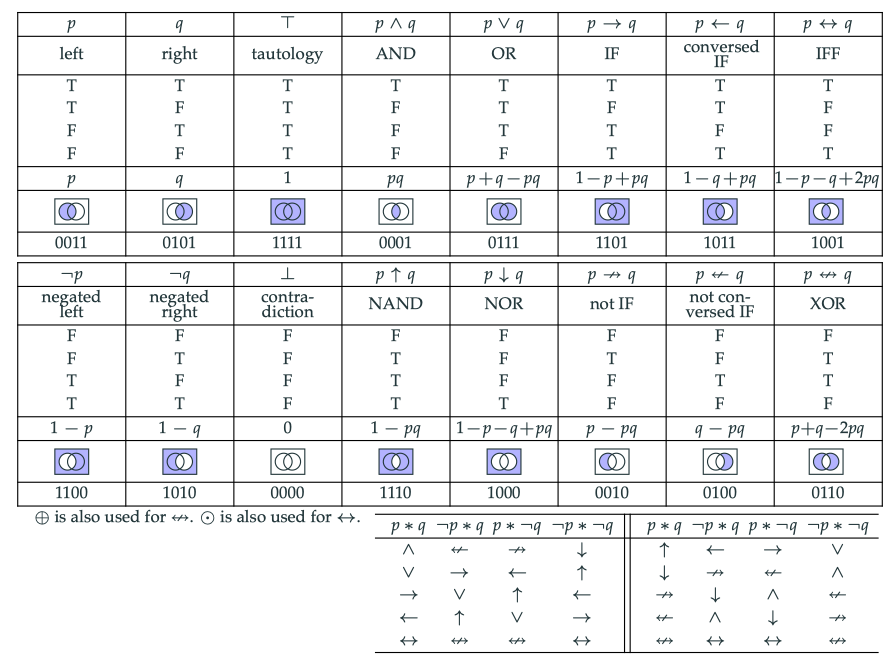
일관성 (Consistent)
명제 변항에 진리값을 할당해 각 명제가 모두 참이 되도록 할 수 있는 경우, 명제 목록은 일관성(consistent)있다.
예졔
세가지 명제가 주어진다.
- “메시지는 저장되거나 재전송된다”
- “메시지는 저장되어있지 않다”
- “메시지가 저장된다면, 재전송된다”
p 는 “메시지가 저장된다”를 나타내고, q는 “메시지가 재전송된다”를 나타낸다면 각 명제는 이렇게 작성할 수 있다.
p ∨ q¬pp → q
이 명제 목록은 p가 거짓, q가 참일 경우 모두 참이 된다. 따라서 이 목록은 일관성있다.
만약 여기서 “메시지가 재전송되지 않음” 명제가 추가된다면?
다음 명제가 추가된다.
¬q
이 경우 변항이 어떤 진리값을 가지더라도 만족하는 할당이 없으므로 일관성을 가지지 않는다.
항진명제, 항위명제, 우발성명제 (tautology, contradiction, contingency)
- 항진명제(tautology) : 항상 참인 명제
- ex.
p ∨ ¬p
- ex.
- 항위명제(contradiction) : 항상 거짓인 명제
- ex.
p ∧ ¬p
- ex.
- 우발성명제(contingency) : 항진명제, 항위명제가 아닌 명제
- ex.
p
- ex.
논리적 동등 (Logically Equaivalent)
p ↔ q 가 항진명제(tuatology)라면, p와 q는 논리적으로 동등(Logically Equaivalent)하다.
이런 논리적 동등을 p ⇔ q 또는 p ≡ q 로 쓴다.
Key logical Equaivalences
Identity Laws (항등 법칙)
p ∧ T ≡ pp ∨ F ≡ q
Domination Laws (지배 법칙)
p ∨ T ≡ Tp ∧ F ≡ F
Idempotent laws (멱등 법칙)
p ∨ p ≡ pp ∧ p ≡ p
Double Negation Law (이중 부정 법칙)
¬(¬p) ≡ p
Negation Laws (부정 법칙)
p ∨ ¬p ≡ Tp ∧ ¬p ≡ F
Commutative Laws (교환 법칙)
p ∧ q ≡ q ∧ pp ∨ q ≡ q ∨ p
Associative Laws (결합 법칙)
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
Distributive Laws (분배 법칙)
(p ∨ (q ∧ r)) ≡ (p ∨ q) ∧ (p ∨ r)(p ∧ (q ∨ r)) ≡ (p ∧ q) ∨ (p ∧ r)
Absorption Laws (흡수 법칙)
p ∨ (p ∧ q) ≡ pp ∧ (p ∨ q) ≡ p
(Involving Conditional Statements)
p → q ≡ ¬p ∨ qp → q ≡ ¬q ∨ ¬pp ∨ q ≡ ¬p → qp ∨ q ≡ ¬(p → ¬q)¬(p → q) ≡ p ∧ ¬q(p → q) ∧ (p → r) ≡ p → (q ∧ r)(p → q) ∨ (p → r) ≡ p → (q ∨ r)(p → r) ∧ (q → r) ≡ (p ∨ q) → r(p → r) ∨ (q → r) ≡ (p ∧ q) → r
(Involving Biconditional Statements)
p ↔ q ≡ (p → q) ∧ (q → p)p ↔ q ≡ ¬p ↔ ¬qp ↔ q ≡ (p ∧ q) ∨ (¬p ∧ ¬q)¬(p ↔ q) ≡ p ↔ ¬q
드모르간 법칙 (De Morgan’s laws)
논리곱의 부정은 각각 부정의 논리합과 같다
논리합의 부정은 각각 부정의 논리곱과 같다
¬(p ∧ q) ≡ ¬p ∨ ¬q¬(p ∨ q) ≡ ¬p ∧ ¬q
충족 가능성 (Propositional satisfiability)
명제를 참으로 만드는 변항의 진리값이 존재할 때, 복합 명제는 satisfiable하다고 한다.
그렇지 않은경우, unsatisfibale하다.
명제의 부정이 항진 명제(tautology)라면, 그 명제는 unsatisfibale하며 그 역도 성립한다.
WIP