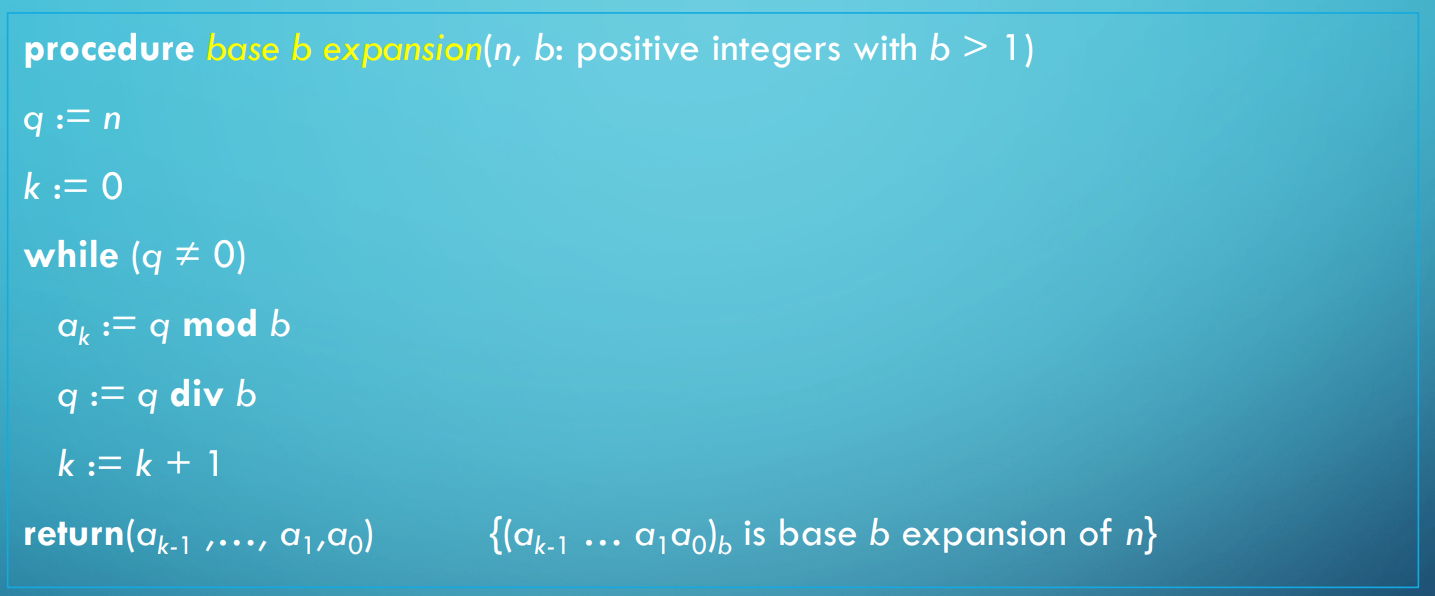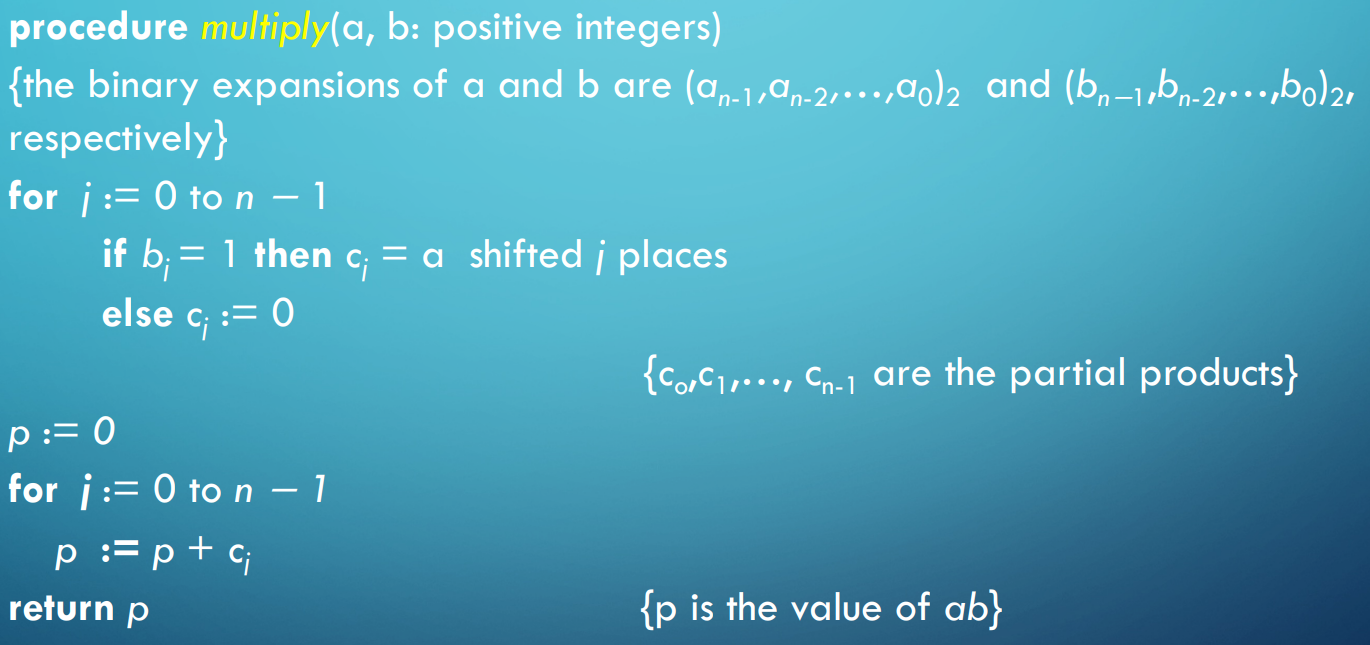Base B Representations
다음 정리를 통해 1보다 큰 양의 정수 $b$을 기준으로 정해 사용할 수 있다
\[n = a_kb^k + a_{k-1}b^{k-1} + a_{k-2}b^{k-2} + a_{k-3}b^{k-3} + ... + a_1b + a_0\]정리 1 : $b$를 1보다 큰 양의 정수라고 하자. 그럼 $n$이 양의 정수일 때, 이는 다음 형식으로 고유하게 나타낼 수 있다
$k$는 음수가 아닌 정수, $a_0,a_1,…a_k$는 $b$ 보다 작은 음수가 아닌 정수이고 $a_k \ne 0$이다.
$a_j, j = 0, … ,k$ 는 base-b digits 표현법 라고 불린다
2진수 확장 (Binary Expansions)
대부분 컴퓨터는 정수를 표현하고 산술 연산을 하는데 2진수를 사용한다 (base 2)
이런 지수에서 사용되는 숫자는 0, 1이다
8진수 확장 (Octal Expansions)
octal expansion (base 8)은 digits {0, 1, 2, 3, 4, 5, 6, 7} 을 사용한다
16진수 확장 (Hexadecimal Expansions)
The hexadecimal expansion은 16개의 digits를 필요로 하므로 알파벳 A-F를 사용한다
base 변환
정수 $n$을 base $b$로 변환하는 방법
- $n$을 $b$로 나누어 몫과 나머지를 구한다
- $n = bq_0 + a_0 (0 \le a_0 < b)$
- 나머지 $a_0$은 Base b 확장의 가장 오른쪽 자리다
- $q_0$을 $b$로 나누어 몫과 나머지를 구한다
- $q_0 = bq_1 + a_1 (0 \le a_1 < b)$
- 나머지 $a_1$는 Base b 확장의 오른쪽에서 두번째 자리다
- 몫이 0이 될때까지 반복한다
의사 코드
이진수 덧셈
의사 코드
이진수 곱셈
의사 코드
Binary Modular
암호학에서 $b,n,m$이 매우 큰 정수일 때, $b^n \mod m$을 찾는 것은 중요하다
$n$의 이진 표현을 사용해, $n = (a_{k-1}, …, a_1, a_0)$이라면, $b^n$을 연산하는 방법은 다음과 같다
\[b^n = b^{a_{k-1} \cdot 2^{k-1} + a_{k-2} \cdot 2^{k-2} + ... + a_1 \cdot 2 + a_0}\] \[= b^{a_{k-1} \cdot 2^{k-1}} \times b^{a_{k-2} \cdot 2^{k-2}} \times \cdots \times b^{a_1 \cdot 2} + b^{a_0}\]그러므로, b^n을 계산하기위해 $b, b^2, b^{2^2}=b^4, b^{4^2}=b^8, …$ 가 필요하다
문제
$3^11$ 을 계산하라
풀이
$11 = (1011)_2$
따라서, $3^11 = 3^8 \cdot 3^2 \cdot 3^1 = ((3^2)^2)^2 \cdot 3^2 \cdot 3^1 = 9^2 \cdot 9 \cdot 3$