홈 이산수학 | Solving Congruences
포스트
취소

이산수학 | Solving Congruences

게시 2023/12/04
By Hve
11 분읽는 시간

선형 합동 (Linear Congruences)

정의 : $m$은 양의 정수, $a, b$는 정수, $x$는 변수일 때 다음과 같은 합동식이 있다

\[ax ≡ b (\mod m)\]

이 식을 선형 합동(linear congruence)이라 부린다

선형 합동 $ax ≡ b (\mod m)$에 대한 해는 합동을 만족하는 모든 $x$가 된다

정의 : $a\tilde{a} ≡ 1 (\mod m)$ 을 만족하는 $\tilde{a}$를 $a \text{ modulo } m$ 의 역원이라 한다

예시

5는 3 modulo 7 의 합동이다

  • $5 \cdot 3 ≡ 15 ≡ 1 (\mod 7)$

    a modulo m 의 역수

다음 정리는 $a$와 $m$이 relatively prime이 될 때마다, modulo m의 역수가 존재한다는 것을 보장한다

정리 1: $a$와 $m$이 relatively prime(서로소)이고 $m$이 1보다 크면, modulo m의 역수가 존재한다

또한 이 역수는 modulo m에서 고유하다

증명

$\gcd(a,m) = 1$ 이므로, $sa + tm = 1$ 인 정수 $s, m$이 존재한다

  • 그러므로, $sa + tm ≡ 1 (\mod m)$ 이다
  • $tm ≡ 0 (\mod m)$ 이므로, $sa ≡ 1 (\mod m)$이다
  • 결과적으로 $s$는 a modulo m의 역수이다

역수 찾기

유클리드 알고리즘과 베주 계수를 통해 역수를 구하는 체계적인 접근법을 사용한다

문제 : 3 modulo 7의 역원

3 modulo 7 의 역원을 찾아라

풀이

$\gcd(3,7) = 1$이므로, 정리 1에 의해 3 modulo 7의 역원이 존재한다

유클리드 알고리즘을 사용한다

  • $7 = 2 \cdot 3 + 1$
  • 위 방정식에 따라 $-2 \cdot 3 + 1 \cdot 7 = 1$

여기서 -2, 1는 Bézout coefficients(베주 계수)로 볼 수 있다

  • 그러므로 3 modulo 7의 역원은 -2다
  • 또한, -2 modulo 7과 합동인 모든 수 또한 역원이다 (5, -9, 12 등…)

문제 : 101 modulo 4620의 역원

101 modulo 4620 의 역원을 찾아라

  1. 먼저 유클리드 알고리즘은 gcd(101, 4620) = 1인지 확인한다
  • $ 4620 = 101 \cdot 45 + 75$
  • $ 101 = 75 \cdot 1 + 26$
  • $ 75 = 26 \cdot 2 + 23$
  • $26 = 23 \cdot 1 + 3$
  • $23 = 3 \cdot 7 + 2$
  • $3 = 2 \cdot 1 + 1$
  • $2 = 1 \cdot 2 + 0$
  1. backward 수행
  • $1 = 3 - 1 \cdot 2$
  • $1 = 3 - 1 \cdot (23 - 3 \cdot 7) = -1 \cdot 23 + 8 \cdot 3$
  • $1 = -1 \cdot 23 + 8 \cdot (26 - 23 \cdot 1) = 8 \cdot 26 - 9 \cdot 23$
  • $1 = 8 \cdot 26 - 9 \cdot (75 - 26 \cdot 2) = 26 \cdot 26 - 9 \cdot 75$
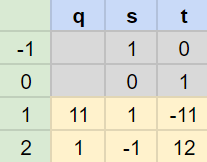
  • $1 = 26 \cdot (101 - 1 \cdot 75) - 9 \cdot 75 = 26 \cdot 101 - 35 \cdot 75$
  • $1 = 26 \cdot 101 - 35 \cdot (4620 - 101 \cdot 45) = -35\cdot 4620 + 1601 \cdot 101$

IMAGE

따라서 101 modulo 4620의 역원은 1601이다

역을 사용해 합동 풀기

도함수 $ax ≡ b (\mod m)$을 양변에 $\tilde{a}$를 곱해 풀 수 있다

예시

$3x ≡ 4 (\mod 7)$을 풀어라

위에서 3 modulo 7의 역원이 -2인것을 구했다. 따라서 양변에 -2를 곱하면

\[-2 \cdot 3x ≡ -2 \cdot 4 (\mod 7)\]

$-6 ≡ 1 (\mod 7)$이고, $-8 ≡ 2 (\mod 7)$ 이므로 $x ≡ -8 ≡ 2 (\mod 7)$ 이다

중국인의 나머지 정리 (CRT, Chinese Remainder Theorem)

존재성 증명

$m = m_1m_2 \cdots m_n$ 이라고 하고, $n_k = \frac{m}{m_k}$라고 하자

$\gcd(n_k, m_k) = 1$이다

그럼 베주 항등식에 의해 $s_kn_k + t_km_k = 1$ 을 만족하는 $s_k, t_k$가 존재한다

따라서, $s_kn_k ≡ 1 (\mod m_k)$ 이다

$x = a_1n_1s_1 + a_2n_2s_2 + \cdots + a_nn_ns_n$ 이라고 하자

$j \ne k$라면 $m_k \mid n_j$ 이고, 따라서 $x ≡ a_kn_ks_k ≡ a_k \cdot 1 = a_k (\mod m_k)$ 이다

유일성 증명

$x, y$가 주어진 연립 합동식의 해라고 가정하자.

그러면

$ x ≡ a_1 (\mod m_1), y ≡ a_1 (\mod m_1)$

$ x ≡ a_2 (\mod m_2), y ≡ a_2 (\mod m_2)$

$\vdots$

$ x ≡ a_n (\mod m_n), y ≡ a_n (\mod m_n)$

이다

그러므로 임의의 $k (1 \le k \le n)$에 대해, $x ≡ a_k ≡ y (\mod m_k)$이고, 따라서 $x - y ≡ 0 (\mod m_k)$이다

lemma에 의해 $\text{lcm}(m_1,m_2,\cdots,m_n) \mid (x-y)$ 이며 $m_1,m_2,\cdots,m_n$ 은 pairwise relatively prime(쌍마다 서로소)이므로 다음과 같다

$m_1,m_2,\cdots,m_n \mid (x-y)$

따라서, $x ≡ y (\mod m_1m_2 \cdot m_n)$이다

예시

다음 식에서 x의 값을 구하라

  • $x ≡ 2 (\mod 3)$
  • $x ≡ 3 (\mod 5)$
  • $x ≡ 2 (\mod 7)$

풀이

  • $m = m_1 \cdot m_2 \cdot m_3 = 3 \cdot 5 \cdot 7 = 105$
  • $n_1 = \frac{m}{m_1} = 35$
  • $n_2 = \frac{m}{m_2} = 21$
  • $n_2 = \frac{m}{m_3} = 15$

베주 항등식을 이용한 역원을 구한다

$\gcd(n_1, m_1)=\gcd(35, 3)=1$

IMAGE

  • $35 \cdot (-1) + 3 \cdot 12 = 1$
  • 35 modulo 3의 역원은 -1

$\gcd(n_2, m_2)=\gcd(21, 5)=1$

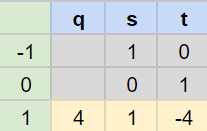
IMAGE

  • $21 \cdot 1 + 5 \cdot (-4) = 1$
  • 21 modulo 5 의 역원은 1

$\gcd(n_3, m_3)=\gcd(15, 7)=1$

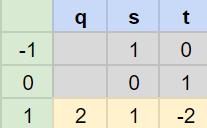
IMAGE

  • $15 \cdot 1 + 7 \cdot (-2) = 1$
  • 15 modulo 7 의 역원은 1

$x = a_1n_1s_1 + a_2n_2s_2 + a_3n_3s_3$ 이므로

$x = 2 \cdot 35 \cdot (-1) + 3 \cdot 21 \cdot 1 + 2 \cdot 15 \cdot 1 = 23$

따라서, $23 (\mod 105)$ 이다

페르마의 소정리 (Fermat’s Little Theorem)

정리 3 : $p$가 소수이고 $a$가 $p$로 나누어지지 않는 정수라면 다음과 같다

\[a^{p-1} ≡ 1 (\mod p)\]

추가로 모든 정수 $a$에 대해 $a^p ≡ a (\mod p)$이다

예시

Find $7^{222} \mod 11$ 찾기

풀이

페르마 소정리에 따라 모든 $k$에 대해 $7^10 ≡ (7^10)^k ≡ 1 (\mod 11)$ 이다

\[7^{222} = 7^{22*10+2} = (7^{10})^{k} \cdot 49 ≡ 5 (\mod 11)\]

그러므로 $7^{222} \mod 11 = 5$ 이다

유사소수

페르마 소정리에 따르면, $2^{n-1} ≡ 1 (\mod n)$ 을 만족하는 $n > 2$인 $n$은 소수이다

그러나, 실제로 $n$는 소수가 아닐 수 있다. 이런 값을 base 2에 대한 유사소수라고 부른다

예시

  • $341 = 11 \cdot 31$
  • $2^{340} ≡ 1 (\mod 341)$

정의 : $b$를 양의 정수라고 하자. 만약 $n$가 합성수이고 $b^{n-1} ≡ 1 (\mod n)$이라면, $n$을 base b에 대한 의사소수라고 한다

유사소수 판별

$2^{n-1} ≡ 1 (\mod n)$에 대해

  • $n$이 합동성을 만족하지 않으면, 합성수이다
  • $n$이 합동성을 만족하면, 소수거나 base 2에 대한 유사소수이다

원시근 (Primitive root)

정의 : Primitive(원시근) modulo p (p는 소수) 이 $r$이라고 하면, $Z_p$의 0이 아닌 모든 원소는 power of $r$이다.

wIP_DN_07_75

예시

$Z_{11}$의 모든 원소는 power of 2이다. 2는 $Z_{11}$에서 원시근이다

  • Power of 2 modulo 11
    • $2^1 = 2$
    • $2^2 = 4$
    • $2^3 = 8$
    • $2^4 = 5$
    • $2^5 = 10$
    • $2^6 = 9$
    • $2^7 = 7$
    • $2^8 = 3$
    • $2^9 = 6$
    • $2^{10} = 1$

$Z_{11}$의 모든 원소는 power of 3이 아니며, 따라서 3은 $Z_{11}$에서 원시근이 아니다

  • Power of 3 modulo 11
    • $3^1 = 3$
    • $3^2 = 9$
    • $3^3 = 5$
    • $3^4 = 4$
    • $3^5 = 1$

Important Fact : 모든 소수 p에 대해 원시근 modulo p가 존재한다

이산 로그

$p$를 소수라고 하고 $r$을 원시근 modulo p라고 하자

$a$가 1과 p-1사이 정수라면, $r^e = a \text{ in } Z_p$를 만족하는 $Z_p$의 원소이며 고유한 거듭제곱 e가 존재한다

정의 : $p$를 소수라 가정하고 $r$을 원시근 modulo p, $a$를 1과 p-1사이 값이라고 하자.

$r^e \mod p = a$ 이고 $1 \le e \le p-1$라면, $e$를 이산 로그(discrete lograithm) of a modulo p to the base r 이라고 하며 다음과 같이 쓴다 : $\text{ld}_r a = e$ (where the prime p is understood)

예시

  • $\text{ld}_2 3 = 8$ : base 2에 대한 3 modulo 11 의 이산로그가 8이다 as $2^8 = 3$ modulo $11$

  • $\text{ld}_2 5 = 4$ : base 2에 대한 4 modulo 11의 이산로그는 5이다 as $2^5 = 4$ modulo $11$

Applications of Congruence

해시 함수

Detail in DN_07_80

의사 난수

Detail in DN_07_81

Check Digits : UPCS

숫자 문자열에서 오류를 감지하는 방법중 하나로 끝에 추가 숫자롤 표기한다

UPC(Universal Product Codes) : 범용 제품 코드

Check Digits : ISBNS

Detail in DN_07_84

공부, 이산수학
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.
바로가기