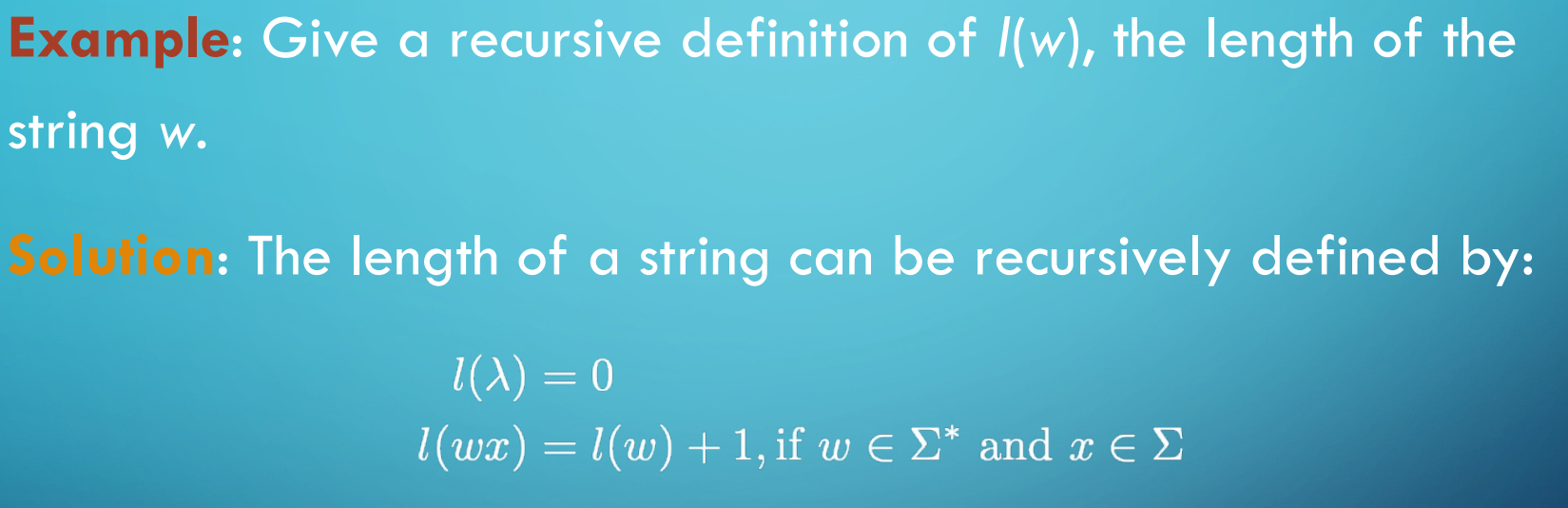재귀적 정의된 함수
정의 : 함수의 재귀적 또는 귀납적 정의는 다음 두 단계로 구성된다
Basis Step : 함수 F(0)의 값을 지정한다
Recursive Step(재귀 단계) : 작은 정수의 값에서 정수의 값을 구하는 규칙을 지정한다
문제 1
Suppose f is defined by: $f(0) = 3$ and $f(n+1) = 2 \cdot f(n) + 3$
Find f(1), f(2), f(3), f(4)
풀이
- $ f(1) = 2 \cdot f(0) + 3 = 2 \cdot 3 + 3 = 9 $
- $ f(2) = 2 \cdot f(1) + 3 = 2 \cdot 9 + 3 = 21 $
- $ f(3) = 2 \cdot f(2) + 3 = 2 \cdot 21 + 3 = 45 $
- $ f(4) = 2 \cdot f(3) + 3 = 2 \cdot 45 + 3 = 93 $
문제 2 : 팩토리얼
팩토리얼 함수 $n!$에 대한 함수를 정의해라
풀이
$f(0) = 1$ and $ f(n+1) = (n+1)f(n) $ for $n \ge 1$
문제 3 : sum
\[\sum_{k=0}^{n}a_k\]다음 재귀 함수를 정의해라
풀이
- $\sum_{k=0}^{0}a_k = 0$
- $\sum_{k=0}^{n+1}a_k = \sum_{k=0}^{n}a_k + a_{n+1}$
피보나치 수
피보나치 수에 대한 정의는 다음과 같다
for $n \ge 2$, $F_0 = 0, F_1 = 1, F_n = F_{n-1} + F_{n-2}$
문제 4 : 피보나치 수
WIP_DN08_37
라메의 정리 (WIP)
라메의 정리 : $a, b$가 $a \ge b$인 양의 정수라고 가정하면, 유클리드 알고리즘으로 gcd를 구하는데 사용하는 나눗셈의 수는 b의 소수점 이하 자릿수의 5배 이하가 된다
WIP_DN_08_38
재귀적으로 정의된 집합 및 구조
집합의 재귀적 정의는 두 단계로 나뉜다
- Basis Step : 초기 컬렉션 지정
- Recursive step : 집합에 이미 있는 것으로 알려진 요소로부터 집합에 새로운 요소를 형성하는 규칙을 제공한다
예제 1
정수 집합의 부분집합 $S$에 대해
- Basis step : $3 \in S$
- Recursive step : if $x \in S$ and $y \in S$라면, $x+y$는 $S$에 속한다
초기에 3이 존재하고, 이후 3+3=6이 존재하고, 3+6=9가 존재하고, 6+6=12가 존재하고, 등등…
예제 2
자연수 $N$에 대해
- Basis step : $0 \in N$
- Recursive step : if $x \in N$이라면, $x+1 \in N$이다
문자열 (Strings)
정의 : 알파벳 $\Sigma 위의 문자열의 $ $\Sigma^*$ 집합은 다음과 같다
- Basis Step : $\lambda \in \Sigma^*$ ($\lambda$ 는 빈 문자열)
- Recursive Step : if $w \in \Sigma^$이고 $x \in \Sigma$라면, $wx \in \Sigma^$이다
예시
If $\Sigma = \set{0, 1}$ 이라면, $\Sigma^*$ 집합의 원소는 다음과 같다 $\lambda, 0, 1, 00, 01, \cdots$
문자열 연결
정의: 연결이라 불리는 연션을 통해 두 문자열을 결합할 수 있다
$\cdot$으로 표시되는 두 문자열의 연결을 재귀적으로 다음과 같이 정의할 수 있다
- Basis Step : $w \in \Sigma^*$, then $w \cdot \lambda = w$
- Recursive Step : $w_1 \in \Sigma^$ and $w_2 \in \Sigma^$, then $w_1 \cdot (w_2 x)$
문자열 길이
균형잡힌 괄호 문제 (Balanced Parenthses)
Well-formed formulae in propositional logic
루트가 있는 트리 (Rooted Tree)
정의 : rooted trees의 집합은 root라 불리는 유한 정점을 포함하는 정점 집합과이러한 정점을 연결한는 엣지 집합으로 구성되며, rooted tree 집합은 다음 단계를 통해 재귀적으로 정의할 수 있다
Basis Step : 단일 정점 하나는 rooted tree이다
Recursive Step
- $T_1, T_2, \cdots T_n$이 각각의 루트 $r_1, r_2, \cdots r_n$을 가진 분리된 루트 트리라고 가정하자.
- 그럼 루트 $r$ ($T_1, T_2, \cdots T_n$ 중 어디에도 속하지 않는)로 시작하여 그래프를 형성하고 $r$ 에서 각각의 정점 $r_1, r_2, \cdots r_n$으로 간선을 추가함으로서 이 또한 루트 트리가 된다
WIP_DN_08_46
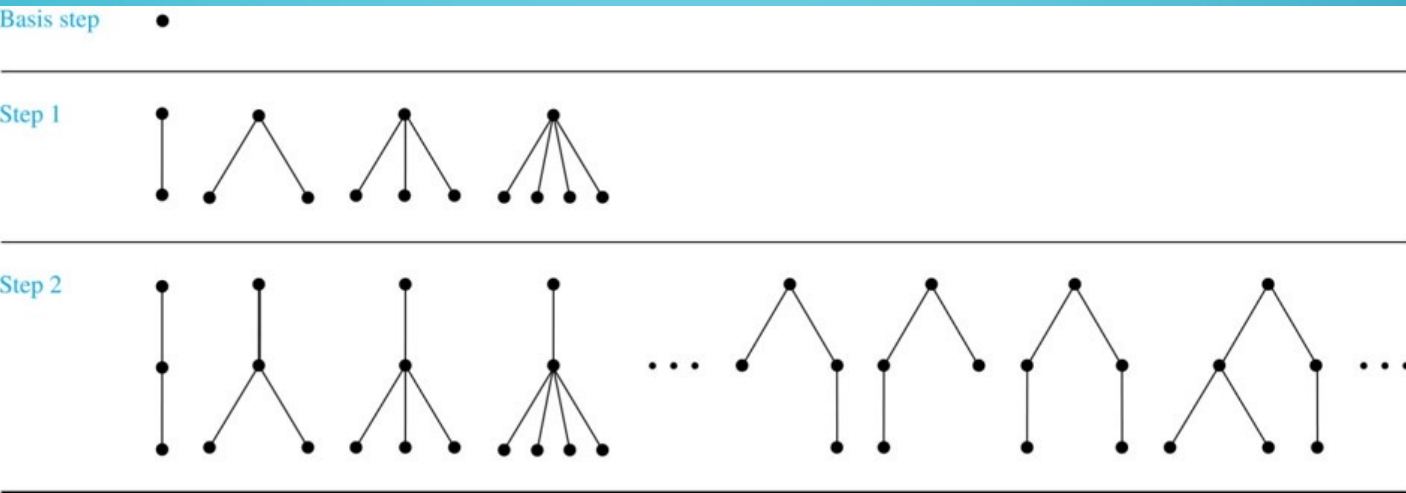
완전 이진 트리 (FULL BINARY TREES)
Basis Step : 단일 정점 하나는 rooted tree이다
Recursive Step
- $T_1, T_2$이 각각의 루트 $r_1, r_2$을 가진 분리된 루트 트리라고 가정하자.
- 그럼 루트 $r$ ($T_1, T_2$ 어디에도 속하지 않는)로 시작하여 그래프를 형성하고 $r$ 에서 각각의 정점 $r_1, r_2$으로 간선을 추가함으로서 이 또한 루트 트리가 된다
귀납 및 재귀적으로 정의된 집합의 잘못된 예시
WIP… (DN_08_P51)
재귀 함수
정의 : 알고리즘이 더 적은 입력으로 동일한 문제의 인스턴스로 축소하여 문제를 해결하는 경우 알고리즘을 재귀적이라고 한다
재귀 팩토리얼 알고리즘
재귀 지수화 알고리즘
$a^n$을 계산하는 알고리즘
재귀 GCD 알고리즘
재귀 모듈러 지수 알고리즘
$b, n, m$ 이 정수이고 $m \ge 2, n \ge 0, 1 \le b \le m$ 일 때, $b^n \mod m$을 계산하기 위한 알고리즘을 고안하라
이진 탐색
WIP_DN08_62
재귀 알고리즘이 올바른지 증명하기
수학적 귀납법과 강한 귀납법은 모두 재귀 알고리즘이 올바른 출력을 생성한다는 것을 보여주는 유용한 방법이다
예제
다음 재귀 지수화 알고리즘이 옳은지 증명하라
풀이
수학적 귀납법을 사용한다
Basis Step : 모든 음수가 아닌 정수에 대해 $a_0 = 1$이다. 그리고 power(a, 0) = 1이다
Inductive Step
- 생략_DN08_P63
Merge Sort
WIP_DN08_P64