이산수학 순열과 조합

비둘기집 원리

비둘기 집 원리 : $K$가 양의 정수이고 $K+1$개의 개체가 $K$개의 상자에 배치되면, 적어도 하나의 상자에는 두개 이상의 개체가 포함된다

일반화된 비둘기집 원리

일반화된 비둘기집 원리 : $N$개의 물체를 $k$개의 상자에 넣으면 최소한 $\lceil N/k \rceil$개의 물체를 포함하는 상자가 하나 이상 있다

증명

대우에 의한 증명을 사용한다

문제

a) 동일한 모양의 카드 3장 이상이 선택되도록 하려면, 52장의 표준 카드 덱에서 몇장의 카드를 택해야 하나? (Club, Diamond, Heart, Spade 문양이 있다)
b) 또, 최소 3개의 하트가 선택되도록 보장하려면 몇개를 택해야 하나?

풀이 (a)

각 문양마다 주어진 4개의 상자를 가정한다. 일반화된 비둘기집의 원리를 사용하면 각 하나 이상의 상자에 최소 $\lceil N/4 \rceil$개의 카드가 있다

$\lceil N/4 \rceil \ge 3$ 인 경우, 한 문양의 카드 3장 이상이 선택된다

$\lceil N/4 \rceil \ge 3$ 이므로, $N = 2 \cdot 4 + 1 = 9$

풀이 (b)

덱에는 하트 카드 13장와 하트가 아닌 카드 39장이 있다

41장을 선택시 하트 2장과 나머지 하트가 아닌 카드 39장이 나올 수 있다

따라서 42장을 선택시 최소 하트 3장이 포함될 수 있다 (여기서 일반화된 비둘기집 원리는 사용되지 않는다)

순열 (Permutations)

정의: 일련의 개별 개체의 순열은 이러한 개체를 순서대로 배열하는 것입니다. 세트의 r개 요소를 순서대로 배열하는 것을 r-순열이라고 합니다.

n개의 원소가 있는 집합의 r-순열을 $P(n,r)$로 쓴다 (한국에서는 $_nP_r$을 사용한다)

순열 정리

정리 1: $n$이 양의 정수이고 $r$이 $1 \le r \le n$인 정수인 경우,

\[P(n, r) = n(n-1)(n-2) \cdots [n-(r-1)]\]

따라서 다음과 같다

\[P(n,r) = _nP_r = \frac{n!}{(n-r)!}\]

증명

곱 규칙을 이용한다

첫 원소는 n개의 방법으로 고를 수 있다. 두번째는 n-1 개 중 고를 수 있다. 마지막 원소는 n-(r-1)개 중 고를 수 있다.

문제

ABCDEFGH 문자의 순열 중 ABC 문자열이 포함된 순열은 몇 개입니까?

풀이

6개의 개체 $\set{ABC, D, E, F, G, H}$ 에 대해 순열을 카운팅하면 된다

\[6! = 720\]

조합 (Combinations)

정의 : r-combination(r-조합)은 집합에서 r개의 요소를 순서없이 선택하는 것이다
n개의 개별 요소로 구성된 집합의 r-조합 수는 $C(n, r)$로 표시되며 이항 계수(binomial coefficient)라고도 한다. 한국에서는 ${n \choose r}$로도 나타낸다

\[C(n,r) = {n \choose r} = \frac{n!}{(n-r)!r!}\]

문제 : 카드 뽑기

52장으로 구성된 카드에서 5장의 카드를 뽑는 가짓수

풀이

\[C(52, 5) = \frac{52!}{47!5!} = \frac{52 \cdot 51 \cdot 50 \cdot 49 \cdot 48}{5 \cdot 4 \cdot 3 \cdot 2}\]

52장으로 구성된 카드에서 47장의 카드를 뽑는 가짓수

풀이

\[C(52, 47) = \frac{52!}{47!5!} = C(52, 5)\]

따라서 5장을 뽑는것과 같다

조합 추론

Corollary : $C(n,r) = C(n,n-r)$

조합적 증명 (COMBINATORIAL PROOFS)

정의 1 : 항등식의 조합적 증명은 다음 방법 중 하나를 사용하는 증명이다

double counting proof : counting arguments를 사용해 항등식의 양쪽을 서로 다른 방식으로 계산하여 보여주는 것
bijective proof : 항등식의 두 방법에 의해 계산된 개체의 집합 사이에 전단사(bijection)가 있음을 보여주는 것

예시

$r, n$이 음수가 아닌 정수인 경우 다음을 증명하라

\[{n \choose r} = {n \choose n-r}\]

증명 (bijective proof)

$S$가 $n$개의 요소로 구성된 집합이라 하자. $S$의 부분 집합 $A$을 $A’$로 매핑하는 함수는 $r$ 요소를 가진 $S$의 부분 집합과 $n-r$요소를 가진 부분집합 사이의 전단사이다. 두 집합 사이에는 전단사가 있으므로, 두 집합의 요소 개수는 동일해야 한다

Double Counting Proof

정의에 따르면, r개의 요소를 갖는 S의 부분 집합의 수는 $C(n,r)$이다. $S$의 각 부분 집합 $A$는, $A$에 없는 요소 $\overline{A}$를 지정하여 설명 할 수 있다.

$r$개의 요소를 갖는 $S$의 부분 집합의 보수는 $n-r$개의 소수를 가지므로, $r$개의 요소를 갖는 $S$의 $C(n, n-r)$ 부분 집합도 존재한다

이항 계수와 항등식 (BINOMIAL COEFFICIENTS AND IDENTITIES)

wIP_DN09_42

이항식의 거듭제곱 (Powers of Binomial Expressions)

정의 : 이항식(binomial expression)은 $x + y$와 같은 두 항의 합이다

counting principle을 사용해 $(x+y)^n$ 전개에서 계수를 찾을 수 있다
$(x+y)(x+y)(x+y)$는 각각의 세 합에서 하나의 항을 곱한 항들의 합으로 확장된다
$x^3, x^2y, xy^2, y^3$ 형태가 나타난다. 계수(coefficient)는 어떻게 되는가?
$x^3$을 얻기 위해서는 각 항에서 $x$가 선택되어야 한다. 이 방법은 하나뿐이므로 $x^3$의 계수는 1이다
$x^2y$를 얻기 위해서는 두 합에서 x가 선택되고 다른 합에서 y가 선택되어야 한다. 이 방법은 $C(3,1)=3$가지가 있다. 따라서 $x^2y$의 계수는 3이다
$xy^2$를 얻기 위해서는 두 합에서 y가 선택되고 다른 합에서 x가 선택되어야 한다. 이 방법은 $C(3,1)=3$가지가 있다. 따라서 $xy^2$의 계수는 3이다
$y^3$을 얻기 위해서는 각 항에서 $y$가 선택되어야 한다. 이 방법은 하나뿐이므로 $y^3$의 계수는 1이다

따라서 $(x+y)^3 = x^3 + 3x^2y + 3xy^2 + y^3$ 이다

이항 정리 (Binomial Theorem)

Binomial Theorem : $x, y$를 변수라고 하고 $n$을 음수가 아닌 정수라고 했을 때 다음과 같다

\[(x+y)^n = \sum_{k=0}^n {n \choose k}x^{n-k}y^k = {n \choose 1}x^n + {n \choose 2}x^{n-1}y + \cdots + {n \choose n-1}xy^{n-1} + {n \choose n}y^n\]

문제 : 이항 정리

$(2x-3y)^{25}$ 에서 $x^{12}x^{13}$의 계수는?

풀이

\[{25 \choose 12}(2x)^{12}(-3y)^{13} = \frac{25!}{12!13!}\cdot2^{12}\cdot(-3)^{13}\]

Useful Identity

Corollay 1: $n \ge 0$일 때, $x, y$라면, 두가지 방법에 의해 다음을 보일 수 있다

이항 정리

\[2^n = (1+1)^n = \sum_{k=0}^n {n \choose k} 1^{n-k}1^{k} = \sum_{k=0}^n {n \choose k}\]

조합론적 증명

WIP_DN_09_45

Pascal’s Identity

Pascal’s Identity : $n, k$가 정수이고 $n \ge k \ge 0$이라면, 다음과 같다

\[{n+1 \choose k} = {n \choose k-1} + {n \choose k}\]

증명 (조합론)

$T$를 집합이라 하고 $\mid T \mid = n+1, a \in T$ and $S=T / \set{a}$라 하자

그럼 $k$개의 원소를 포함한 $T$ 집합의 ${n+1 \choose k}$개의 부분 집합이 존재한다

WIP_DN_09_45

일반화된 순열 및 조합

반복과 순열

정리 1: 반복이 허용되는 n개의 객체에 대한 r-순열의 개수는 $n^r$개

반복과 조합

정리 2: 원소의 반복이 허용될 때, 고유 원소가 n개인 집합으로부터 r-조합의 수는 다음과 같다

\[{n+r-1 \choose r} = {n+r-1 \choose n-1}\]

증명

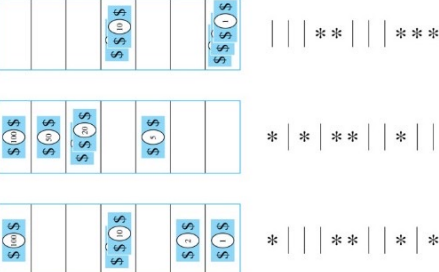
원소의 반복이 허용되는 n개의 원소가 있는 집합의 각 r-조합은 n-1개의 막대와 r개의 별의 목록으로 나타낼 수 있다

문제 : 박스에서 지폐 꺼내기

각각의 1달러, 2달러, 5달러, 10달러, 20달러, 50달러, 100달러가 5장 이상씩 든 상자에서 5개의 지폐를 선택하는 방법은?

해결

지폐 5장을 선택하는 방법의 수는 막대 6개와 별5개를 연속으로 선택하는 것과 동일하다

이것은 11개의 집합에서 5개의 개체를 순서없이 선택하는 것이다

따라서 ${11 \choose 5} = \frac{11!}{6!5!} = 462$ 가지 방법이 있다

문제 : 방정식의 해 구하기

$x_1, x_2, x_3$가 음수가 아닌 정수일때 다음 방정식에서 해가 몇개 존재하는가?

\[x_1 + x_2 + x_3 = 11\]

해결

각 해는 3가지 원소를 가진 집합에서 11개의 항목을 선택하는 방법에 해당한다

따라서 정리 2에 따라 다음과 같이 풀 수 있다

\[{11 + 3 - 1 \choose 11} = {13 \choose 11} = {13 \choose 2} = 78\]

문제 : 쿠키

4가지 종류의 쿠기가 있다고 했을 때, 6개 쿠키를 선택할 수 있는 방법은?

해결

6개의 쿠키를 선택할 수 있는 방법의 수는 4개의 요소가 있는 세트의 6가지 조합의 수이다

\[{4+6-1 \choose 6} = {9 \choose 6} = {9 \choose 3} =84\]

반복의 유무에 따른 순열, 조합

Type	반복	공식
r-순열	No	$_nP_r$
r-조합	No	$_nC_r = {n \choose r}$
r-순열	Yes	$\prod_{n}^{r} = n^r $
r-조합	Yes	$_nH_r = {n+r-1 \choose r}$

구별할수 없는 객체의 순열

정리 3: 구별할 수 없는 각각의 객체가 각각 $n_1$개, $n_2$개, $n_3$개 $\cdots$ 있고 전체 객체의 수가 $n$개라면, 서로 다른 순열의 개수는 다음과 같다

\[\frac{n!}{n_1!n_2! \cdots n_k!}\]

풀이

곱의 규칙에 따라 순열의 총 개수는 다음과 같다

\[C(n,n_1)C(n-n_1,n_2) \cdots C(n-n_1-n_2 \cdots - n_)\] \[\frac{n!}{n_1!(n-n_1)!} \cdot \frac{(n-n_1)!}{n_2!(n-n_1-n_2)!} \cdots = \frac{n!}{n_1!n_2! \cdots n_k!}\]

문제 : 구별할수 없는 객체의 순열

‘SUCCESS’라는 단어의 글자를 재배열해 몇 개의 다른 글자를 만들 수 있나?

풀이

3개의 S, 2개의 C와, 1개의 U, E가 있다

3개의 S는 C(7, 3)가지 방법으로 배치할 수 있다
2개의 C는 C(4, 2)가지 방법으로 배치할 수 있다
1개의 E, C(2, 1)가지 방법으로 배치할 수 있다
1개의 U, C(1, 1)가지 방법으로 배치할 수 있다

따라서 다음과 같다

\[{7 \choose 3}{4 \choose 2}{2 \choose 1}{1 \choose 1} = 420\]

물건을 상자에 분배하기

물체는 서로 다르거나 동일하다 (구별 가능/불가능) (Distinguishable/Indistinguishable)
상자에 라벨이 붙어 있거나 붙어있지 않음 (구별 가능/불가능)

구별 가능한 객체와 구별 가능한 상자

\[\frac{n!}{n_1!n_2! \cdots n_k!}\]

구별 불가능한 객체와 구별 가능한 상자

$C(n+r-1, n-1)$ 가지 방법이 있다

예시: 10개의 구별 불가능한 물체를 8개의 구별 가능한 상자에 넣는 방법은 $C(17, 10)$ 가지이다

구별 가능한 객체와 구별 불가능한 상자

해당 분배를 위한 간단한 공식은 없다

예시: 4명의 직원을 구분 불가능한 3개의 방에 넣는 방법은 14가지이다

4명이 한 방에 있는 경우 : 1가지
3/1명으로 나뉘는경우 : $C(4,1) = 4$가지
2/2명으로 나뉘는 경우 : $C(4,2)/2 = 3$가지
2/1/1명으로 나뉘는 경우 : $C(4,2)C(2,1)C(1,1)/2 = 6$

구별 불가능한 객체와 구별 불가능한 상자